Trong thực tiễn cuộc sống cũng như trong khoa học kĩ thuật, người ta cần phải tính diện tích của những hình phẳng cũng như thể tích của những vật thể phức tạp. Chẳng hạn:

- Khi xây dựng một nhà máy thủy điện, để tính lưu lượng của dòng sông ta phải tính diện tích thiết diện ngang của dòng sông. Thiết diện đó thường là một hình khá phức tạp.

- Khi đóng tàu, các kĩ sư cần xác định thể tích của khoang tàu có hình dạng đặc biệt.

Sự ra đời của tích phân cho chúng ta một phương pháp tổng quát để giải hàng loạt những bài toán tính diện tích và thể tích nói trên.

I. Tính diện tích hình phẳng

1. Hình phẳng giới hạn bởi một đường cong và trục hoành

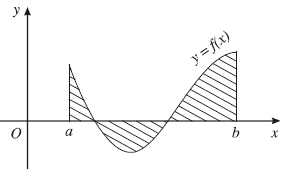
$\begin{array}{l} \left. {\left( {u\left( x \right)v\left( x \right)} \right)} \right|_a^b - \int\limits_a^b {u'\left( x \right)v\left( x \right)dx} \\ S = \int\limits_a^b {\left| {f\left( x \right)} \right|} dx \end{array}$

2. Hình phẳng giới hạn bởi hai đường cong

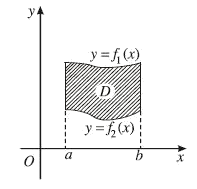
$S = \int\limits_a^b {\left| {{f_1}\left( x \right) - {f_2}\left( x \right)} \right|} dx$

II. Tính thể tích

1. Thể tích của vật thể

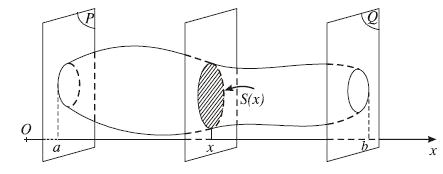
$V = \int\limits_a^b {S\left( x \right)} dx$

2. Thể tích khối chóp và khối chóp cụt

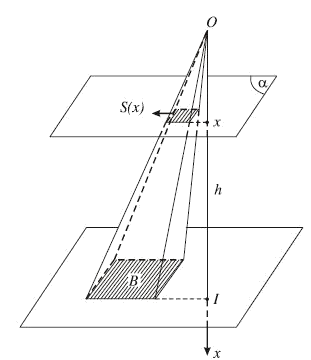
$V = \int\limits_0^h {B\frac{{{x^2}}}{{{h^2}}}} dx = \frac{{Bh}}{3}$

III. Thể tích khối tròn xoay

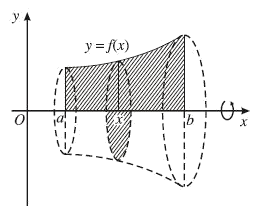
$\begin{array}{l} \int\limits_a^b {u\left( x \right)v'\left( x \right)dx}  = \left. {\left( {u\left( x \right)v\left( x \right)} \right)} \right|_a^b - \int\limits_a^b {u'\left( x \right)v\left( x \right)dx} \\ V = \pi \int\limits_a^b {{f^2}\left( x \right)} dx \end{array}$